Skip to content

Interlude #1: Cellular automata

This isn't a coding tutorial. That's why I called it an interlude. This is a gentle exploration of cellular automata.

A cellular automaton is a system of cells in a grid, each containing a numerical value that changes over time according to a rule. Visualisations of automata typically use colours to represent the different values or states of a cell. By applying a transformation rule over and over, these visuals often reveal intricate patterns, ranging from repetitive mosaics to seemingly organic structures. The best known example is the Game of Life.

The universe of the Game of Life is a two-dimensional grid with cells that can be in two states: zero or one, dead or alive, white or black. I wanted to create a simulation of a different automaton; one with a single dimension, but with cells that can be in three states. Each iteration of the system corresponds to a row of cells, and we can stack the rows to visualise the evolution over time.

A coloured grid of cells, containing triangular patterns.
Example of a one-dimensional automaton with three states: white, green, or black. The system starts at the top with a single green cell. Each horizontal line represents an iteration or a generation. This system reveals triangular patterns over the first 150 generations.

In most cases, a cell changes state depending on its own value and the value of its immediate neighbours. A rule defines how that happens. If a cell has one of three possible values, the combination of a cell with its left and right neighbours can be in 33 or 27 states. The rule simply maps each of those states onto a resulting value for the cell. Below is an illustration of a rule, which we'll come to know as rule 136.

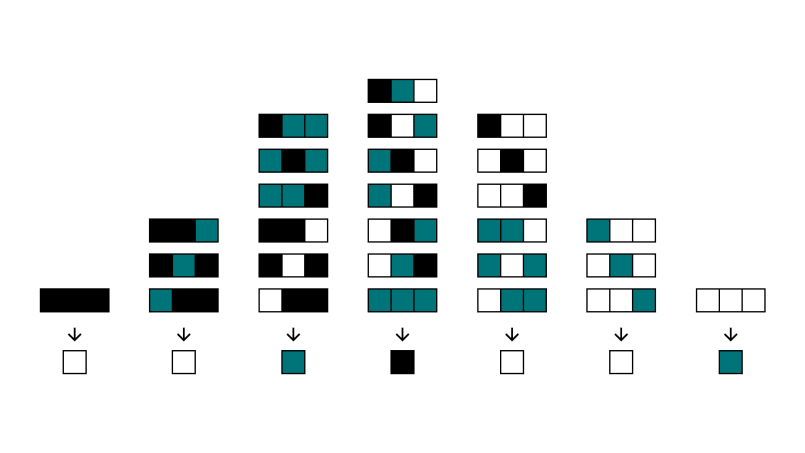
A diagram showing all the possible combinations of three squares in three colours, and the way in which they're transformed into another colour.
Example of a rule. Each possible configuration of a cell and its neighbours is mapped onto another value.

The automaton I'm making is a so-called totalistic automaton. That means the next value depends on the total of the values of the cell and its neighbours. Say white, green and black correspond to zero, one and two. Then the combination black-green-green has a total value of 2 + 1 + 1, or four; and is in that sense identical to black-white-black, which also sums to 2 + 0 + 2, or four. With zero (white-white-white) being the lowest and six (black-black-black) the highest sum, a rule will have to assign a next state to seven initial states. That leaves room for 37 or 2187 different rules. One of those is rule 136, which I illustrated earlier. Let's revisit the image and add some numbers to clarify that this is indeed a valid rule:

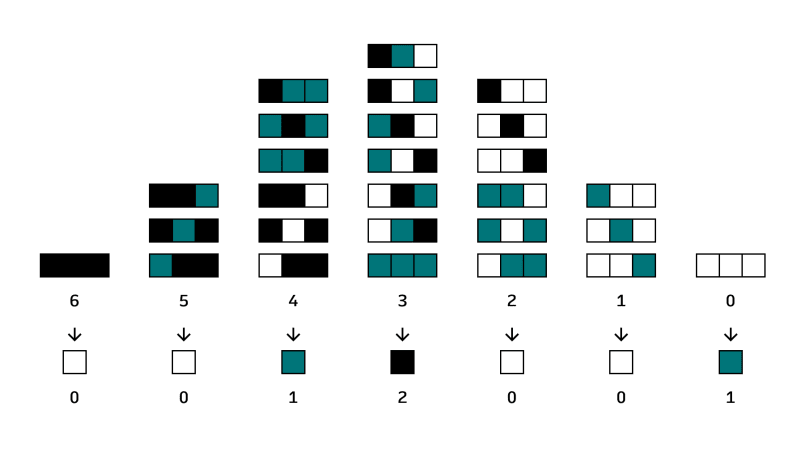
A diagram showing all the possible sums of the values of three cells, and the way in which they're mapped onto another value.
The rule assigns a value to each of seven possible sums.

The order in this diagram, with the highest sum on the left and the lowest on the right, might give a hint as to why we call this rule 136. The number 136 is the decimal representation of the ternary number 0012001, which corresponds to the rule at the bottom of the diagram. Think of it as 0 × 36 + 0 × 35 + 1 × 34 + 2 × 33 + 0 × 32 + 0 × 31 + 1 × 30, which is 81 + 2 × 27 + 1, or indeed 136.

Each of the 2187 rules has a different effect on the system. Broadly, we can observe four types of behaviour:

  • The system becomes homogenous. A single colour remains.
  • The system becomes cyclical. A pattern repeats.
  • The system becomes chaotic. There's no apparent pattern.
  • The system becomes locally complex. Parts of the grid exhibit complex behaviour while other parts are homogenous or cyclical.
A coloured grid showing mostly one colour.
Homogenous system.
A coloured grid showing a repeated pattern.
Cyclical system.
A coloured grid showing triangles of different sizes without any apparent repetition.
Chaotic system. There's a triangular pattern, but we can't discern a repetition or a cycle.
A coloured grid showing triangles of different sizes without any apparent repetition, and a patch of solid green.
Locally complex system.

Below is our automaton. You can fiddle around to discover distinct patterns and behaviours. The simulator starts with a single green cell, and evolves according to rule 136. You can use the controls to start or pause the automaton, to change the rule, or to inject some randomness into the system.

Rule 593 is particularly nice, with its almost biological feel. If you're on a desktop, it's fun to use the up and down arrows in the number input to quickly cycle through different rules. Inject some randomness from time to time if the system evens out. Have fun!